Financial Modeling: Using Triangular Distribution

In financial modeling one of  more used functions in business decision-making is the triangular distribution. This function is very practical because it includes business knowledge of the experts. It only needs three elements from them: their worst, most likely, and best scenario. 

The challenge: I was able to solve a financial model with uncertainties without using @Risk and VBA. My project has two uncertainties: Sales and growth. 

• The first year of sales: Min=80, Max=200, Mode= 170 million units
• Growth rate from 2Y-5Y: Min=3%, Max=8%, Mode=5%

Additional information: Investment=$50 million, Infl.=2%, p=$0.20, c=$0.08

Based on this information I built the model to get the NPV. I used the triangular function to include managers’ perception about sales and growth. To complete the simulation I created a data table to iterate 1000 times the NPV outcomes.

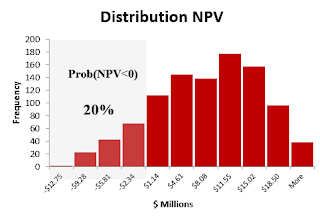
The main results:

• Mean NPV=+$6.6 million with a 95% of chance that this mean will be between $6.1 and $7.0 million.
• 20% of probability of losses (NPV<0).

Some useful tricks: 

• Excel does not include a triangular function, so it is necessary to install a free add-in that can be found here. This add-in also includes a large number of optimized probability functions. I hope the next Excel version will include a triangular function in its library. 
• New function: NtRandTriangular(X,Min,Max,Mode). It is a random generator for a triangular distribution. X is the number of interactions that we want to simulate (1000). It creates internally a vector with the size of X. 
• Excel function: Index(vector,n). This function allows me to extract the specific interaction from the vector NtRandTriangular.
• In the data table the NPV is the final outcome. In order to get new NPVs for each row I linked to the interaction number; this will update and save the new NPV.

Here is the Excel file with the project (link).
If you found this helpful, please share.